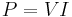Joule heating

Joule heating, also known as ohmic heating and resistive heating, is the process by which the passage of an electric current through a conductor releases heat. It was first studied by James Prescott Joule in 1841. Joule immersed a length of wire in a fixed mass of water and measured the temperature rise due to a known current flowing through the wire for a 30 minute period. By varying the current and the length of the wire he deduced that the heat produced was proportional to the square of the current multiplied by the electrical resistance of the wire.

$Q \propto I^2 \cdot R$

This relationship is known as Joule's First Law. The SI unit of energy was subsequently named the joule and given the symbol J. The commonly known unit of power, the watt, is equivalent to one joule per second.

It is now known that Joule heating is caused by interactions between the moving particles that form the current (usually, but not always, electrons) and the atomic ions that make up the body of the conductor. Charged particles in an electric circuit are accelerated by an electric field but give up some of their kinetic energy each time they collide with an ion. The increase in the kinetic or vibrational energy of the ions manifests itself as heat and a rise in the temperature of the conductor. Hence energy is transferred from the electrical power supply to the conductor and any materials with which it is in thermal contact.

Joule heating is referred to as ohmic heating or resistive heating because of its relationship to Ohm's Law. It forms the basis for the myriad of practical applications involving electric heating. However, in applications where heating is an unwanted by-product of current use (e.g., load losses in electrical transformers) the diversion of energy is often referred to as resistive loss. The use of high voltages in electric power transmission systems is specifically designed to reduce such losses in cabling by operating with commensurately lower currents. The ring circuits, or ring mains, used in homes are another example, where power is delivered to outlets at lower currents, thus reducing Joule heating in the wires. Joule heating can be defeated using superconducting materials.

Resistors create electrical noise, called Johnson–Nyquist noise. There is an intimate relationship between Johnson–Nyquist noise and Joule heating, explained by the fluctuation-dissipation theorem.

1 Formulas and proof
- 1.1 Direct current
- 1.2 Alternating current
2 Reason for high-voltage transmission of electricity
3 Applications
- 3.1 Self-heating thermistors
4 Heating efficiency
5 References
6 See also

Formulas and proof

Direct current

The most general and fundamental formula for Joule heating is:

$P=VI$

where

P is the power (energy per unit time) converted from electrical energy to thermal energy,
I is the current traveling through the resistor or other element,
V is the voltage drop across the element.

The explanation of this formula (P=VI) is:^[1]

(Energy dissipated per unit time) = (Energy dissipated per charge passing through resistor) × (Charge passing through resistor per unit time)

When Ohm's law is applicable, the formula can be written in other equivalent forms:

$P=IV=I^2R=V^2/R$

where R is the resistance.

Alternating current

Main article: AC power

When current varies, as it does in AC circuits,

$P(t)=I(t)V(t)$

where t is time and P is the instantaneous power being converted from electrical energy to heat. Far more often, the average power is of more interest than the instantaneous power:

$P_{avg}=I_{rms}V_{rms}=I_{rms}^2R=V_{rms}^2/R$

where "avg" denotes average (mean) over one or more cycles, and "rms" denotes root mean square.

These formulas are valid for an ideal resistor, with zero reactance. If the reactance is nonzero, the formulas are modified:

$P_{avg} = I_{rms}V_{rms}\cos\phi = I_{rms}^2 R = V_{rms}^2 G$

where $\phi$ is the phase difference between current and voltage, R is resistance (i.e., the real part of impedance Z), and G is conductance (i.e., the real part of admittance). On the other hand, for elements with reactance,

$P_{avg} \neq V_{rms}^2/R$

For more details in the reactive case, see AC power.

Reason for high-voltage transmission of electricity

Main article: Electric power transmission

In electric power transmission, high voltage is used to reduce Joule heating of the overhead power lines. The valuable electric energy is intended to be used by consumers, not for pointlessly heating the power lines. Therefore this Joule heating is referred to as a type of transmission loss.

The power station wants to transfer a certain amount of electrical power P_load through power lines. (P_load represents the power used by all the elevators, televisions, etc. served by the station.) Since $P_{load}=I_{rms}V_{rms}$ (ignoring phase difference, see AC power), it is possible to deliver the same power using a higher current at a lower voltage, or a lower current at a higher voltage. Transformers can switch between one and the other method of power transmission.

Since 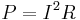$P=I^2R$ , using very low current at a very high voltage is the best way to reduce the transmission loss associated with Joule heating of the power lines. This explains the use of high voltage in the electrical grid.

The formula $P=V^2/R$ seems to suggest, incorrectly, that high voltage increases transmission losses. However, it is important to use the correct V: V is the slight reduction in voltage between the two sides of the power line, also called "line drop"; V is not the "line voltage" relative to ground.^[1] The line drop decreases when the line voltage increases (for a fixed power transmission).

Applications

An incandescent light bulb glows when the filament is heated by Joule heating, so hot that it glows white with thermal radiation (also called blackbody radiation).

Electric stoves and other electric heaters usually work by Joule heating.

Soldering irons and cartridge heaters are very often heated by Joule heating.

Self-heating thermistors

Thermistors and resistance thermometers are resistors whose resistance changes when the temperature changes. These are sometimes used in conjunction with Joule heating (also called self-heating in this context): If a large current is running through the resistor, the resistor's temperature rises and therefore its resistance changes. Therefore, these components can be used in a circuit-protection role similar to fuses, or for feedback in circuits, or for many other purposes. In general, self-heating can turn a resistor into a nonlinear and hysteretic circuit element. For more details see Thermistor#Self-heating effects.

Heating efficiency

Main article: Electric heating

As a heating technology, joule heating has a coefficient of performance of 1.0, meaning that every 1 watt of electrical power is converted to 1 watt of heat. However, a heat pump can be have a coefficient of more than 1.0. For example, if the coefficient of performance is 2.0, then each 1 watt of electrical power will add 2 watts of heat into one volume (say, the inside of a house), while taking 1 watt of heat out of another volume (say, the colder outdoor environment).

Therefore, resistive heating is less efficient than a heat pump. However, it is much simpler to construct, and also easier to integrate into a building. For example, in order to warm a house with a heat pump, the heat pump must have access to both indoor and outdoor air. (It could be located on an outer wall, or with piping.) A resistive heater does not need this.

Compared to heating by burning oil, gas, wood, or other fuels, resistive heating is usually considered less efficient, in the following sense. A power plant burns fuel to create heat, but converts only a fraction of that heat into electrical energy. The electrical energy is transmitted to the building with the resistive heater, where the energy is turned into heat. However, if the fuel was burned directly in the building where the heat was needed, instead of at the power plant, then 100% of the fuel's heat would be put to good use. This helps explain why fuel-burning is a cheaper source of heat than resistive heating in many places. However, this is just one consideration. Other factors are relevant as well, such as the different costs of transporting electricity versus fuel, and the fact that the power plant may be using a different fuel or energy source than the building would use.

References

^ ^a ^b Electric power systems: a conceptual introduction by Alexandra von Meier, p67, Google books link